Reševanje rekurzivnih enačb
Jakob Valič, Fakulteta za matematiko in fiziko, UL
Jakob.Valic@student.fmf.uni-lj.si 

V prispevku si bomo ogledali reševanje rekurzivnih enačb s pomočjo programa Mathematica. Najprej bomo reševali preproste primere enačb, podanih na rekurzivni način. Gre za enačbe, kjer je naslednji člen podan s prejšnjim. Zato je zaporedje odvisno od začetnega člena.
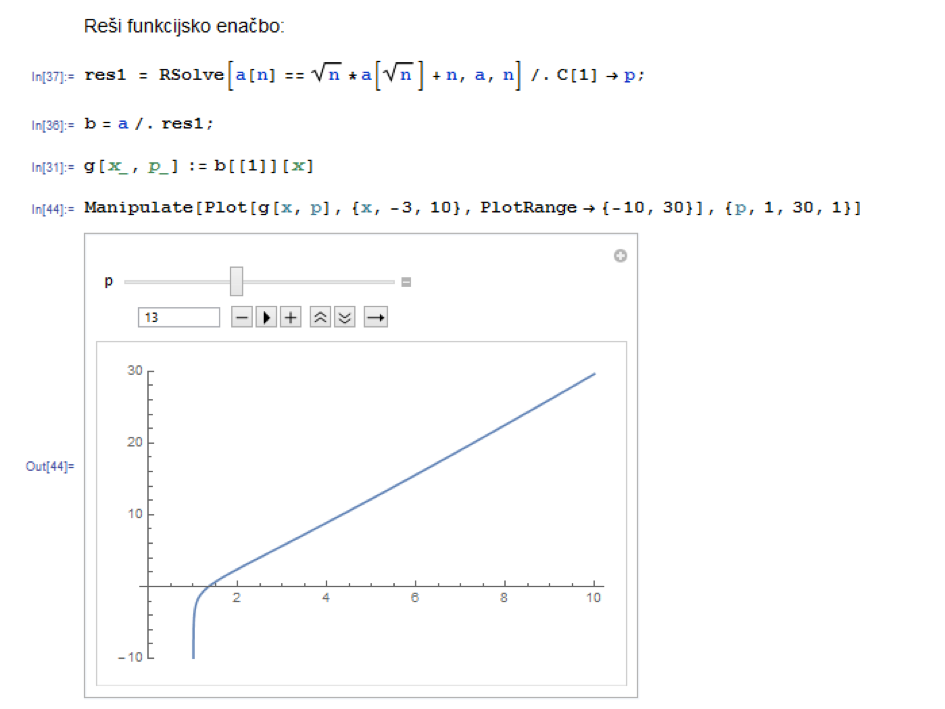
Uporabljali bomo funkcijo RSolve, s katero Mathematica določi splošni člen zaporedja. Splošni člen je natančno določen v primeru, ko podamo tudi začetni člen zaporedja, ponavadi označen z a0. Če tega člena ne poznamo, nam Mathematica vrne splošni člen zaporedja, ki v svoji formuli vključuje eno ali več konstant, označenih s C[1], C[2] itd. Te konstante lahko naknadno določimo s pomočjo prepisovalnih pravil. Na sliki imamo en primer funkcijske enačbe, kjer smo poljubno določili konstanto.
Rekurzivno podano zaporedje lahko napišemo tudi v obliki funkcije. Zato tako zaporedje lahko tudi napišemo kot funkcijo in jo posledično tudi narišemo v obliki grafa. Z uporabo funkcije Manipulate lahko spreminjamo vrednost konstante, npr C[1] in posledično se spreminja tudi graf funkcije. Na koncu si bomo pogledali še praktično uporabo reševanja rekurzivnih enačb, in sicer pri računanju korakov, potrebnih za premestitev n-obročev pri igri Hanojski stolpi; drugi primer bo iz obrestnih mer.
Spoznali bomo tudi funkcijo RSolveValue, s pomočjo katere prav tako računamo splošni člen zaporedja ali funkcijo, ki jo lahko predstavimo v koordinatnem sistemu.