Eulerjeva premica in trilinearni koordinatni sistem
Jure Srabotnik, Fakulteta za matematiko in fiziko, UL
jure.srabotnik@student.fmf.uni-lj.si 

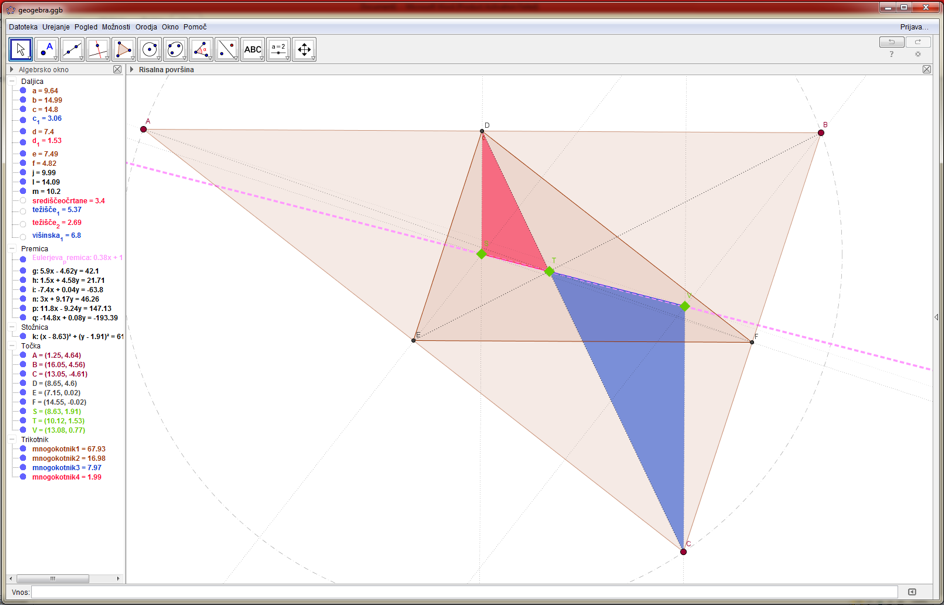
Eulerjeva premica je v geometriji premica v poljubnem neenakostraničnem trikotniku, ki poteka skozi posebne točke trikotnika. Ene izmed teh so: višinska točka, središče trikotniku očrtane krožnice in težišče trikotnika. S pomočjo podobnih trikotnikov bom dokazal, da višinska točka, središče očrtane krožnice in težišče trikotnika ležijo na isti premici.

Pri dokazovanju si bom pomagal s trilinearnim koordinatnim sistemom. Trilinearni koordinatni sistem opisuje lege točk glede na dani trikotnik. Trilinearne koordinate opisujejo relativne razdalje do treh stranic trikotnika; zato niso enolično določene, saj če jih množimo s poljubnim neničelnim realnim številom dobimo ponovno trilinearne koordinate dane točke.

S trilinearnimi koordinatami točk bom ugotovil ali so le-te res kolinearne, saj so poljubne tri točke A, B, C s trilinearnimi koordinatami $a_1:a_2:a_3,b_1:b_2:b_3,c_1:c_2:c_3$ kolinearne samo če je determinanta $M = \begin{vmatrix}a_1 & a_2 & a_3\\b_1 & b_2 & b_3\\c_1 & c_2 & c_3\end{vmatrix}$ enaka nič.