Reševanje rekurzivnih formul in enačbe
Žiga kadunc Kastelec, Fakulteta za matematiko in fiziko, UL
ziga.kadunc-kastelec@student.fmf.uni-lj.si 

V predstavitvi bom predstavil reševanje rekurzivnih enačb s pomočjo programa Mathematica. Gre za enačbe zaporedij, katerih naslednji člen je podan s kombinacijo prejšnjih (prejšne dane vrednosti).

Pri predstavitvi bom uporabljal funkcijo Rsolve. Mathematica določi splošni člen zaporedja. Ta splošni člen je natančno določen v primeru, ko podamo tudi začetni člen zaporedja ali pa tudi preden začnemo funkcijo pisati lahko določimo prvi/prosti člen. Ta pa je označen z $a_0$.

Če tega člena ne poznamo, nam Mathematica vrne splošni člen zaporedja, ki v svoji formuli vključuje eno konstanto ali več konstant, ki označenih s C[1]. Konstante lahko mi sami določimo v funkciji ali pa jih tudi dodamo prej. Namesto funkcije Rsolve lahko uporabimo RsolveValue. Med njima ni velike razlike (oklepaji). Ta (zaporedja) formule ali enačbe lahko pišemo v funkcije ki potem lahko iz te enačbe/forumle/funkcije predstavimo graf, kako bi to zgledalo.

Primer:


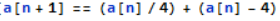
To je splošni člen zaporedja: Zraven smo dobili še onstanto ker ni določenega člena


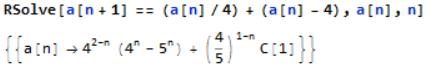
Člen lahko določimo v enačbi ali pa pred njo:


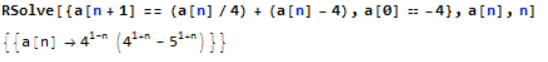
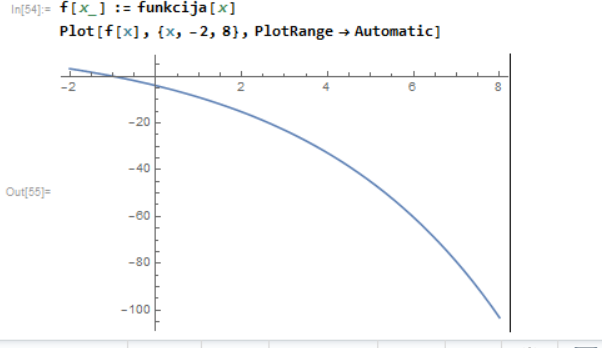
Lahko še grafično prikažemo: Plot