MATHEMATICS AND MUSIC
Frequency is the number of oscillations in one second. The measuring unit for one frequency is s-1, or as it is commonly referred to 1Hz (Hertz). The human ear can transform the undulation of air into sound in the range from 16 to 20000 Hz.
The C-minor scale is part of the West-European tonal range, in which music has been written for more than three hundred years. Let us have a look at the table of approximate frequencies (f) for the tones in the first octave. X denotes the distance of the tone from the first C-tone. One octave is thus represented by tones that are 12 units apart.
|
NOTA |
C |
D |
E |
F |
G |
A |
H |
C |
|
x |
0 |
2 |
4 |
5 |
7 |
9 |
11 |
12 |
|
f |
262 |
294 |
330 |
349 |
392 |
440 |
494 |
523 |
With the aid of the following DERIVE instructions calculate the function that fits the given points best:
Notation:=Decimal
NotationDigits:=5
modify_to_a_b_on_t(data_):= VECTOR([data_ SUB k SUB 1,
LN(data_ SUB k SUB 2)],k,
1,DIMENSION(data_))
res(p_):=FIT(APPEND([[x,a*x+b]],modify_to_a_b_on_t(p_)),x)
BB(r):=LIM(r,x,0,0)
AA(r):=LIM(r,x,1,0)-LIM(r,x,0,0)
powfit(data,x):=APPROX(#e^BB(res(data))*(#e^AA(res(data)))^x,5)
If we want to produce the regression curve, we type the vector with pairs of data:
meritve:=[[0,262],[2,294],[4,330],[5,349],[7,392],[9,440],[11,494],[12,523]]
Then we enter the expression
powfit(meritve,x)
and Simplify it.
The function that fits the given points best calculated by your teacher (on a slightly different way) is: f(x) = 262Χ1,06x. You can use the function you got with the procedure above or use the teacher's one.
How many octaves would there have to be on a piano
which could play all the tones in the human hearing range? Write the two necessary equations, express x and solve the equations.
The equation for the lowest frequency is (f being the lowest frequency we can hear):
. . . . . . . . . . . . .
Express x from the above equation:
.. ..
Calculate x with the help of the DERIVE: x =
The equation for the highest frequency is (f being the highest frequency in the human hearing range):
.
Express x: . .
Solve the equation: x = .. ..
Now we know, how far from the base C tone the two tones corresponding the lowest and highest frequencies are. Therefore we can calculate the number of octaves on our imaginary piano that could play all the tones in the human hearing range.
The number of octaves:
.
Due to its pleasant sound, the
interval called the fifth appears in many folk songs throughout Europe. This
interval is a pair of tones with the frequencies 
. As any such couple is called the fifth, we shall calculate
the one that begins with the tone with the frequency of 440Hz (tone a1).
This tone has been chosen, as it is the starting tone by international
standards. A legend goes that in the Old ages a huge Memnons pillar close to
the Egyptian Thebes emitted the a1 tone every morning at
dawn. That was how the musicians of those times tuned their instruments.
However, the pillar stopped emitting the sound sometime around the birth of
Christ. Luckily, nowadays we can tune our instruments with the help of the
tuning fork, which emits the tone with the frequency of 440Hz. The tuning fork
is even more convenient as it can be carried around (can you imagine having to
go to Greece before every concert).
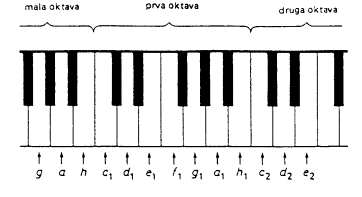
Which tone therefore has to be added to the a1 tone in order to get the fifth?
The equation: .. ..
Express x from the above equation: : .
Solve the equation and round the solution up or down to the nearest whole number:
x = ..
Which tone belongs to the x you have calculated? .