DIMENSIONS OF THE FRACTALS

Between the late 1950s and early 1970s Benoit Mandelbrot evolved a new type of mathematics, capable of describing and analysing the structured irregularity of the natural world, and coined a name for the new geometric forms: fractals. Fractals are forms with detailed structure on every scale of magnification. The simplest fractals are self-similar. Small pieces of them are identical to the whole. We are going to see only some very simple examples.

Some pictures:

The dimension of the fractal is very interesting. We are used to the idea, that a line is one-dimensional, a plane two-dimensional, a solid three-dimensional. But in the world of fractals, dimension aquires a broader meaning, and need not be a whole number.

We are going to study the dimensions of the fractals on the example of Sierpinski gasket. This is obtained by repeatedly deleting the middle quarter of a triangle, removing smaller and smaller pieces, forever. The Sierpinski gasket can be thought of as being composed of three identical gaskets, each half the size of the original.

Dimension d of the fractal is the quotient , where N is the number of new identical shapes and r is the similar proportion between the whole shape and its smaller piece. In our example:

EXERCISES:

Sierpinski gasket

We get it with removing the inner triangle and repeating the procedure on remaining triangles.

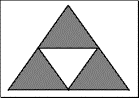
A fractal described by Sierpinski in 1915. It is also called the Sierpinski sieve or Sierpinski triangle.

First we will draw the picture of it. The function describing the points of the gasket has to be made. We just follow the procedure how the gasket is made. So type in the following expression.

TRI_S(u,v,w,n) :=

IF(n=0,[u, v, w, u],

[TRI_S(u, (u+v)/2, (u+w)/2, n-1),

TRI_S(v, (v+w)/2, (v+u)/2, n-1),

TRI_S(w, (w+u)/2, (w+v)/2, n-1)])

Enter

TRI_S([-4,-3],[0,3],[4,-3], 3)

and Simplify the expression. You will get a huge expression describing one stage of Sierpinski's gasket. Now let's draw it. Switch to Plot window and make there some modifications of the settings (Options/Display/Axes – turn everything off, Options/Display/Points – Connect:Yes, Options – turn off Change Plot Colors). Now we are ready! Plot.

Before returning to Algebra window delete the plot (Edit/Delete All Plots).

Repeat the procedure with TRI_S([-4,-3],[0,3],[4,-3], n), where n goes from 0 to 5. Do you know what does n designate? _______________________

Print your picture with n = 4 and colour the gaskets which are not removed.

Calculate the dimension of the Sierpinski gasket.___________

We are going to calculate the circumference and area of the gasket in the fourth class. What do you suppose?

circumference: o = ____________________

area: p = __________________________

Snowflake (Koch's curve)

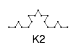
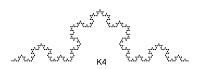
One of perhaps the most famous fractals is Koch's curve named after Helge von Koch, 1904. We start with line (Koch curve of 0th order). We divide the line into three parts. The middle part is substituted with two lines that form an equilateral triangle with deleted line. We got Koch curve of the 1st order. If we apply the procedure on all four lines, we get Koch curve of 2nd order.

Here we have two different variants of Koch's curve. The one ending with 1 is more efficient, but requires a little more knowledge about DERIVE. Newertheles, you can use whichever you want.

TT(a,b):=a+(b-a)/3

TDT(a,b):=TT(b,a)

TO(a,b):=(a+b)/2+SQRT(3)/6*[a SUB 2-b SUB 2,b SUB 1-a SUB 1]

KOCH1(a,b,n) := IF(n=0,[a,b],[KOCH1(a,TT(a,b),n-1),

KOCH1(TT(a,b),TO(a,b),n-1),

KOCH1(TO(a,b),TDT(a,b),n-1),

KOCH1(TDT(a,b),b,n-1)])

KOCH(a,b,n) := IF(n=0,[a],APPEND(KOCH(a,TT(a,b),n-1),

KOCH(TT(a,b),TO(a,b),n-1),

KOCH(TO(a,b),TDT(a,b),n-1),

KOCH(TDT(a,b),b,n-1)))

KOCH_CURVE(a,b,n) := IF(n=0,[a,b],APPEND([a],KOCH(a,b,n))

KOCH_CURVE1(a,b,n) := KOCH1(a,b,n)

Find a dimension of the snowflake curve (of Helge von Koch). You will draw it with plotting simplifed expression KOCH_CURVE([-2,-2],[2,2],n), where n can be any natural number. Of course higer the n is, more time it takes for DERIVE to calculate and draw the corresponding curve.

Print a snowflake curve with n = 4.

If n = 0, we get _____________________.

How many straight lines do we get in the case of n = 1 ? ________

How long is one part? ______________

Dimension of the snowflake curve is d = = ____________

If we draw three Koch curves on corners of equilateral triangle, we get so called Koch snowflake. First let us define POLY(n) which produces corners of a proper polygon of order n.

POLY(n):=VECTOR([3*COS(i),3*SIN(i)],i,2*pi,0,-2*pi/n)

Now we define KS which produces collection of Koch curves between consecutive points of vector a

KS(a,m):=VECTOR(KOCH(a SUB i,a SUB (i+1),m),i,1,DIMENSION(a)-1)

If we Simplify KS(POLY(3), 5) and plot the expression, we get Koch's snowflake. You can experiment by combining different Koch's curves to get various snowflakes. Print the nicest pictures of them.

Menger sponge

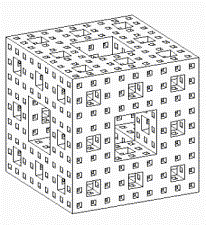
We get it with repeatedly deleting the middle quarter of a cube. A cube divided into 27 subcubes reduced by 7. Each of the remaining subcubes has been treated in the same way as the original cube. The procedure has been repeated analogously. This can go on and on infinetely. Each higher level results in decrease of volume and increase of surface at an exponential rate. For mathematic details visit Eric Weisstein's World of Mathematics (http://mathworld.wolfram.com/MengerSponge.html).

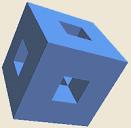
Its dimension is 2,727... Can you prove this?

d = _________________________________________________

Cantor's set

Iteratively removing the middle third of an initiating straight line, as in the Koch curve, ...

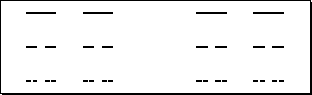
Is it possible to guess the dimension of the Cantor set?

The dimension is between _____ and_____.

Prove:

5.) Are you sure that a line is one-dimensional?

We use a straight line and divide it on n pieces. We don´t remove or add anything. What do we get using the formula d = ?___

Make another proof for a plane!

Sierpinski carpet

A fractal which is constructed analogously to the Sierpinski gasket, but using squares instead of triangles.

Calculate its dimension. ______________________________

Peano's curve

Observe the procedure described with pictures.

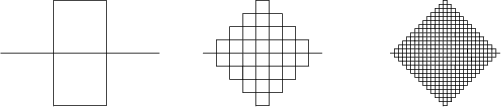
a.) Calculate its dimension. ______________________________

b.) You have got a whole number. How can you explain this?

____________________________________________________

Peano-Gosper curve

Belongs to a family of so called space filling curves. Observe the procedure described with pictures.

a.) Calculate its dimension. ______________________________

b.) You have got a whole number. How can you explain this?

If you want to calculate some more dimensions of fractals, look on

http://forum.swarthmore.edu/advanced/robertd/lsys2d.html

where you can find some additional interesting pictures.

CONCLUSION

Computer graphics is one of the earliest application of fractals. Fractal geometry allows biologist to quantify the surface of important biological molecules (polio virus, iron-bearing protein with d = 1.7, protein of hemoglobin with d = 2.4) , and relate it to their function. The distribution of galaxies within a thousand light years of the Earth is fractal, too (dimension is 1.2).

The appropriate concept of fractal dimension seems to vary from one application to another. An important mathematical problem is to understand how all these various dimensions relate to each other. Much is still not undestood.