SLOVENE FINAL EXTERNAL EXAMINATION – MATURA IN THE VIEW OF COMPUTER ALGEBRA SYSTEMS

Matija Lokar

University of Ljubljana, Faculty of mathematics and physics, Jadranska 19, 1000 Ljubljana, Slovenia, Matija.Lokar@fmf.uni-lj.si

Mojca Lokar

Gimnazija Kranj, Koroška c. 13, 4000 Kranj, Slovenia

Abstract

In Slovenia students have to pass an external examination (called the Matura – "the maturity Exam") at the end of high school as a prerequisite for studying at University. The examination consists of five subjects (three compulsory and two chosen by the student). Mathematics is a mandatory one. At the moment the usage of graphic calculators as well as those with symbolic algebra capabilities is forbidden during the examination. In the view of emerging usage of CAS, we will take a look at one of the last exams. We will classify the questions according to three schemes which measure the usefulness and the impact of computer algebra systems on exam questions.

About Matura

In Slovenia we have various types of secondary education programmes. The Gymnasium (4 years duration) prepares students (15 years +) for higher education (in most cases university studies or higher professional studies) and ends with the Matura examination. Students must pass the Matura examination at the end of the final year as a prerequisite for studying at university. The Matura consists of five subjects, three of which are compulsory (the mother tongue, mathematics and a foreign language), the other two are chosen by the student. Questions are prepared externally and are the same for all grammar schools. The final examination is a school-leaving 'maturity' exam as well as the entry examination to higher education [Budin, Gaberšček 1999a; Budin, Gaberšček 1999b] .

Mathematics and foreign languages are offered at two levels of difficulty: standard and higher. The higher level has additional content and more depth. The candidates who take the subject at the higher level are awarded extra points in the overall grading for the Matura examination. At the higher level, the candidates take another question paper in addition to the papers at the standard level.

80% of the points in mathematics are from the written exam, which is prepared and marked externally, 20% of the points are given in oral examinations that are prepared externally but marked internally.

At the moment the usage of graphic calculators as well as those with symbolic algebra capabilities is forbidden during the examination.

Examination and CAS

Computer algebra systems (CAS) inenvitably influence teaching and learning of mathematics. One of the most debated question that arise from this fact is the influence on assesesment. This question is especially important where examinations are public and external. Various approaches are present nowadays, ranging from the one present in Slovenia (CAS and graphical calculators are forbidden) to those requiring the possesion of a graphical calculator (US in Advanced Placement Calculus examination). Some tests merely allow the use of such technological tools (they tend to produce graphic calculator neutral examinations), in the other ones students are expected to have a graphics calculator (graphic calculator active examinations), yet another type of examinations expects or allows the usage of CAS in one part and forbids the use of any tool in the other part of the exam. When deciding which approach to use, one possible and reasonably obvious stepping stone is to start with the existing examination papers and see what difference having access to a computer algebra system might make.

In the paper we will take a look at the last standard level test exam, used as a preparation for the students passing the examination (Matura) at the end of the 1999/2000 school year. The test is construced in a similar manner as "the real one". We will classify the questions according to two schemes proposed by V. Kokol – Voljč [Kokol 1999, Kokol 2000] and using the categorisation scheme of P. Jones and B. McCrae [Jones 1995; Jones, McCrae 1996]. We will assume that DERIVE for Windows 5 is used.

Traditional examination questions (like the ones in our test exam) can be classified with respect to their significance for testing abilities and skills. Kokol [Kokol 1999, Kokol 2000] proposed the following categories:

[KOin] CAS – insensitive questions
for these questions the use of any calculation tool is of very limited help. Focus is on understanding the underlying mathematical concepts.

[KOch] Questions changing with technology
The main focus is changed when CAS is allowed. These questions usually involve a lot of calculations, and performing those calculations is often more important than the actual goal of the problem. Using CAS for calculations often drastically devalutes the question as its main purpose was to test the calculating abilities of the student. We should therefore pay attention to the ratio between technical/routine work and conceptual understanding.

[KOde] Questions devaluated with CAS
With questions that only test the student's knowledge of calculation procedures all that remains is the testing of the technical ability to use the CAS.

[KOba] Questions testing basic abilities and skills
These questions are mostly connected with transforming expressions from one type to another, using various mathematical rules. Besides the skill of using transformations, knowledge about the structure of expressions is also needed. As CAS performs transformations in its own way some of those questions are still useful for testing with CAS.

Another way of looking at examination questions is how CAS are used in the process of solving them. Kutzler prosposed the following matrix scheme, described in [Kokol 1999, Kokol 2000]

	Routine CAS use	Advanced CAS use
Primary CAS use	KUpr	KUpa
Secondary CAS use	KUsr	KUsa
No CAS use	CUnu

with the follownig meaning:

• Primary CAS use: using a CAS is the major acitivity, problem can hardly be (or even cannot be) solved without the CAS.
• Secondary CAS use: the major emphasis is on abilities CAS does not posses.
• Routine CAS-use: basic knowledge of CAS is sufficient in solving the problem.
• Advanced CAS use: detailed knowledge of CAS is needed.
• No CAS use: CAS is of no help in solving the problem.

Jones [Jones, 1995; Jones, McCrae, 1996] found that questions in traditional examinations appear to fall in three reasonably distinct catagories. He uses his scheme with graphic calculators, but it can be used with CAS too. The categories are:

[JOni] No impact – CAS has no impact on questions as it either contributes nothing to the completion of the task or no more than the allowed tools (scientific calculator).

[JOim] Impact – CAS provides the student with an alternative, but still mathematically valid, method of solution

[JOtr] Trivialization – CAS effectively trivialises the question because it provides a method that only requires a technical skill of using the CAS and little or no mathematical input from the student.

Of course, as with all descriptive schemes, these three have several possible shortcomings as well. The precise meaning of, for example, detailed knowledge depends on the evaluator (an example of this fact is clearly described in [Jones, McCrae, 1996]) . All three schemes are often much too rough and a detailed explanation of the classification of the particular question is necessary to clarify the situation.

The test

In the paper we will take a look at the last test exam, used as a preparation for the students passing examination at the end of the 1999/2000 school year. The test is aimed at the standard level –to be taken by all students. It has 12 questions. For each one we state:

• the exercise, as it appeared in the test;
• its intention: we try to describe the purpose of the exercise, what it tests. As the test was prepared externally, our description, which is based on the proposed marking scheme, can vary from the exact intention of those who prepared the test;
• solution with the help of DERIVE, where we tried to stay at the basic level of the knowledge of the program;
• categorization according to all three schemes: as it has already been mentioned this is a subjective classification and can be argued about;
• Categorization according to all three schemes;
• Value of the exercise with symbolic helper: according to the intention described as well as to the categorization we trided to value the exercise in its present form and
• proposed change if symbolic computation is allowed. Some brief remarks how to (if necessary) change the exercisse to stay as much as possible within "the spirit and intention" of the question. Each exercise is considered separately from the others and we are aware this is a serious drawback as the test should be considered in its entirety.

1. Calculate the exact value of the expression .

Intention: To see if students are able to calculate the expressions with rational exponents.

Solution with DERIVE: Entering the expression sufficies. We must know how to use exponents (Z). Unfortunately we get the right result even if we forget the parentheses around (-1/2) in the exponent. So there is no need to even know the structure of the expression.

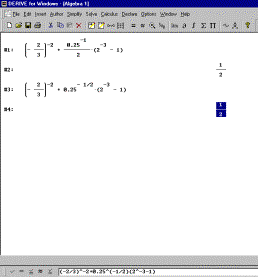
Categorization: KOde (should be KObe but due to the mistake of the pesron who prepared the question is not), KUpr (the deficiency of this scheme I that there is no category for questions which are trivialized with CAS usage), JOtr.

Value of the exercise with symbolic helper: Almost none.

Proposed change if symbolic computation is allowed: We should at very least use an expression where possible mistakes in the order of the operations should not lead to the right answer. The expression could be more complicated; also the root sign should sometimes be used. With symbolic computation the main task left is how to enter the expression (the priority of operations and the structure of the expression) and the equivalence of expressions.

2. The ellipse with the equation is rotated for 90 degrees around the origin of the coordinate system. Write the expression of the ellipse obtained as well as its foci.

Intention: Basic facts about the ellipse and rotation.

Solution with DERIVE: DERIVE can draw the ellipse directly from the expression. The student must know how to change the minor and major axis in the expression. Alternatively symbolic computation can help us to put the expression into the form. Now the student must know how to write the new expression . Also to calculate the foci, we should know that if the ellipse lies along the y-Axis the coordinates of focus are (0, c) and (0, -c) with a² - b² = c² (the last formula is written on the first page of the test).

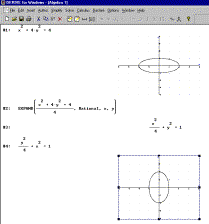
Categorization: KOin, KUsr, JOim.

Value of the exercise with symbolic helper: Symbolic tools are merely tools, all necessary mathematical knowledge is required to solve the exercises successfully.

Proposed change if symbolic computation is allowed: Unnecessary.

3. The rectangle ABCD with the area of 31.5 cm² is divided into a square and a rectangle with the shorter side 2.5 cm long, as can be seen from the picture. Calculate the length of the sides of the rectangle ABCD.

D C

A 2.5 cm B

Intention: Usage of quadratic equation or of a system of two linear equations.

Solution with DERIVE: If we know how to write down the necessary equation, solving it is an elementary task. Then we must know how to interpret the results and drop the negative result.

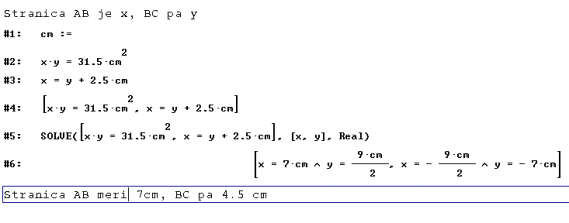
Categorization: KOch, KUsr, JOim.

Value of the exercise with symbolic helper: To get to the quadratic expression we have to posses the necessary mathematical knowledge as well as know how to interpret the results and use units of measurement. Afterwards we do not test if the student knows how to solve the expression (according to the official marking scheme one third of the points can be achieved for this) by hand.

Proposed change if symbolic computation is allowed: Unnecessary, assuming we do not test the knowledge of solving quadratic equations. Perhaps we should change the numbers so that the superficial result of the quadratic equation is not the negative value of the other solution.

4. The functions and are given. Draw the graphs of functions f and g in the coordinate system given below. Calculate the abscises of the intersection points.

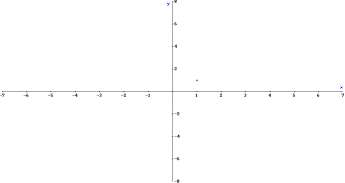
Intention: Graphing the linear function, calculation of the intersection points of the linear functions.

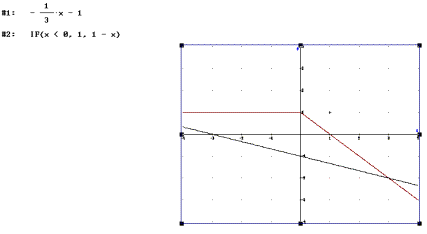
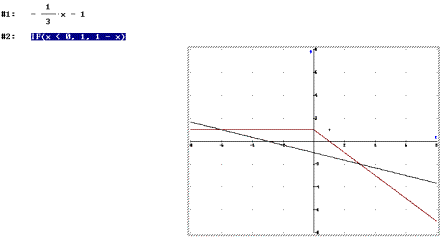
Solution with DERIVE: Producing the graph of the first function is a straightforward task. To get the second graph we must know how to use the IF function, or draw two graphs (1, 1-x) and be careful to use the appropriate parts. As the prescribed coordinate system goes from –7 to 7 on the x-Axis we must also know how to scale the graph. If we use theTrace mode solutions can be easily seen and afterwards merely tried in the equations.

If we use the IF expression, solving cannot be done automatically. So two equations are written. All results are appropriate (there are no intersection points outside the domain space of the function g).

Categorization: KOde, KUpr, JOtr.

Value of the exercise with symbolic helper: As graphing is a crucial part of this exercise, it cannot be used in the present form. Also as the intersection points are "nice", they can be read out from the graph.

Proposed change if symbolic computation is allowed: We should at least use g (x) in the form where the solution of the equation is out of the domain space and where intersection points are not so "nice" (whole numbers). To test the knowledge of graphing the opposite exercise is perhaps more appropriate –write the function given a graph; although there is still the possibility of checking the solution by a program and making the necessary modifications.

5. Write all complex numbers z satisfying the equation .

Intention: Basic fact about complex numbers. Solving complex equations. To express a complex number in the form x + iy or re^ij.

Solution with DERIVE: A direct solution of the equation is not possible. We have to know how to express a complex number with x + iy and how to read the system of equations (transformation of the equation is obtained directly with DERIVE).

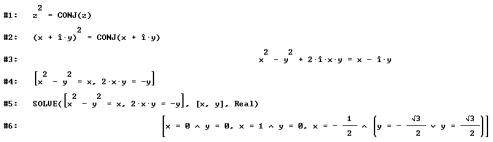
Categorization: KOch, KUsr, JOim.

Value of the exercise with symbolic helper: Depends on what is being tested. If we only want to see whether the student knows the basic procedures, DERIVE in the present state gives a hand exactly where it is appropriate. If we want to test the student's algebraic ability to solve such equations, the exercise is inappropriate.

Proposed change if symbolic computation is allowed: Unnecessary if basic knowledge about complex numbers and the ability to present crucial steps in solving procedure are tested. Otherwise this sort of exercise is obsolete.

6. A polynomial is given. Calculate zeroes and stationary points as well as draw the graph.

Intention: Basic facts about polynomial functions.

Solution with DERIVE: A completely straightforward task. Using Factor, Solve, Differentiate and Plot immediately produces answers. We only have to know that stationary points are zeroes of the first derivative.

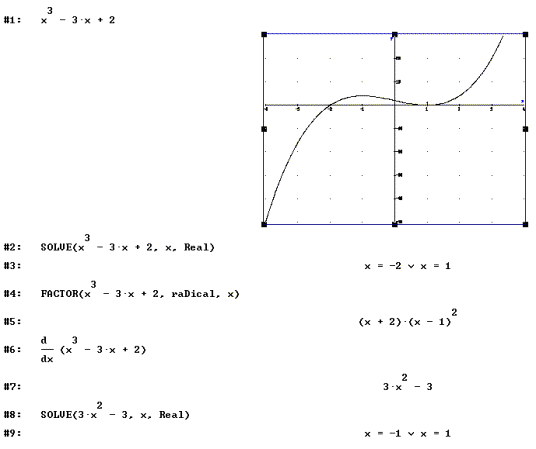
Categorization: KOde, KUpr, JOtr.

Value of the exercise with symbolic helper: Almost none.

Proposed change if symbolic computation is allowed: The exercise should be completely redesigned to achieve proper testing.

7. In the arithmetic sequence the first term equals 2, the n^th term is 302 and the sum of the first n terms is 15352. Calculate n and the difference d of this sequence.

Intention: Testing knowledge about arithmetic sequence.

Solution with DERIVE: We must know that the k^th term equals a_k=a₁+(k-1)d as well as that _. Afterwards the calculation is an easy one, we merely solve two linear equations. If we do not know the second formula, we can use DERIVE to calculate the sum of first n terms, then we express the n^th term and solve the system of two linear equations with DERIVE.

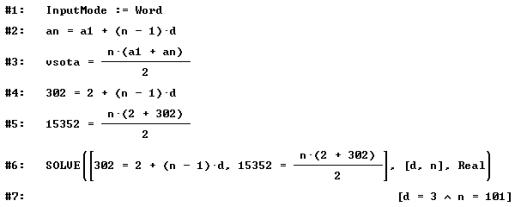
Categorization: KOin, KUsr, JOni.

Value of the exercise with symbolic helper: DERIVE's tasks are elementary ones and perhaps more time is spent on entering the formulas than it would be if the exercise was solved without the help of CAS. The toughest computational task is solving the equation . Perhaps DERIVE can help us to get the second formula, but we should be able to see that 2a₁ + d (n - 1) is equal to a₁ + a_n. If the exercise is supposed to test the knowledge of solving the linear equations as well, we can't use symbolic systems.

Proposed change if symbolic computation is allowed: Perhaps unnecessary. Even with a symbolic system the main property of arithmetic sequence – how the terms are expressed must be known. The "Guide for marking the exam" allows both ways of solving, so the knowledge of the second formula is not required. Of course, since the authors of the exercise assume that symbolic computation is allowed they could use numbers that do not produce such "nice" results.

8. Solve the expression

Intention: Solving logarithmic equations.

Solution with DERIVE: With Solve we only have to write the equation and get the answer immediately.

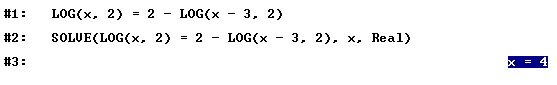
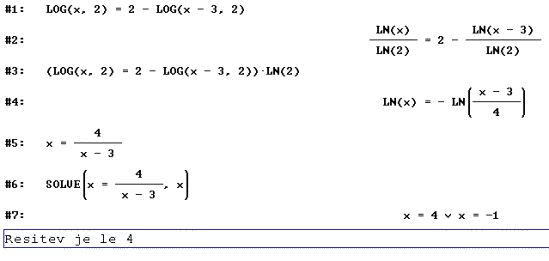
Categorization: KOde, KUpr, JOtr.

Value of the exercise with symbolic helper: None if Solve is allowed.

Proposed change if symbolic computation is allowed: If we want to stay at this type of exercise, Solve should not be allowed. If we want to produce the formula in the form x(x-3) = 4 we must make several steps just to get to the expression LN(x) = -LN((x – 3)/4) and funaly to x = 4 / (x - 3). A student who performs all that steps probably knows the required formulas very well too. Of course DERIVE helps us to solve the equation, but we still have to know that the solution x = -1 is superficial. So without Solve, all crucial parts are still tested with this exercise. With symbolic computation we also have the advantage of being able to use Solve to check our answers – and thus see immediately that there is perhaps something wrong with the solution –1.

9. In the class there are 15 girls and 10 boys. They willrandomly chose a graduation ball committee with three members. Calculate the probability that both sexes will be represented in the committee.

Intention: Basic probability with combinations.

Solution with DERIVE: We use the function COMB.

Categorization: KOin, KUsr, JOni.

Value of the exercise with symbolic helper: DERIVE only helps us in calculating binomial coefficients. So the main part is still mathematical knowledge

Proposed change if symbolic computation is allowed: Unnecessary if we do not insist that students know how a binomial coefficient is calculated.

10. Calculate the angle between the unit vectors and if the vector is orthogonal to the vector .

Intention: Knowing that unit vectors have the length of 1, the connection between dot product and orthogonality.

Solution with DERIVE: We have to produce the formula . Solve then helps us to get three different solutions and the student should observe that the angle is the same one and that different values depend on the way it is measured.

Categorization: KOch, KUsr, JOim.

Value of the exercise with symbolic helper: DERIVE helps us to solve the basic equation.

Proposed change if symbolic computation is allowed: Not necessary. Of course, it could be argued that the students should memorize that cos(p/4)= 1/Ö2. But as DERIVE gives us three answers perhaps using it is also a disadvantage. Also, ordinary calculators are allowed.

11. Show that the equation is true for all x.

Intention: How to prove something. Using various trigonometric formulas.

Solution with DERIVE: We have to make the necessary steps here by ourselves. With solve we see that the equation is really true, but we know that already. Simplification changes the equation to . Afterwards we have to set Trigonometry := Collect to obtain and prove the formula.

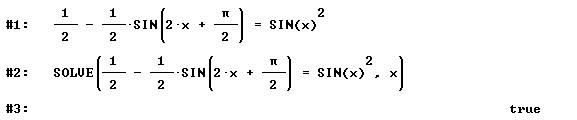
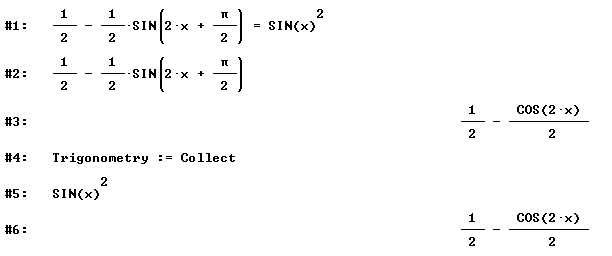
Categorization: KOba, KUsr, JOim.

Value of the exercise with symbolic helper: Without DERIVE we have a little more work combining the formulas (all the necessary ones are given on the first page of the test). But we must know exactly what we wish to do to get DERIVE to simplify the expression into the required format. Possessing this knowledge probably means you also have the required mathematical knowledge.

Proposed change if symbolic computation is allowed: Not necessary.

12. Ball jumps so that in n-th jump reaches the height meters. Write the height reached at the first and at the 10^th jump to the nearest millimeter. In which jump does it reach the height of 1.5m?

Intention: Using exponents, solving exponential equation.

Solution with DERIVE: Write the formula, use Simplify/Variable substitution and approximate. With Solve we get the answer immediately.

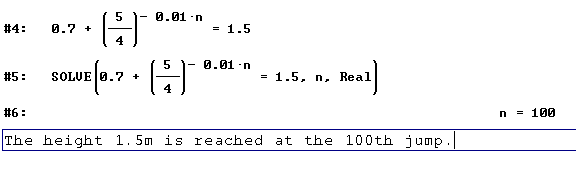
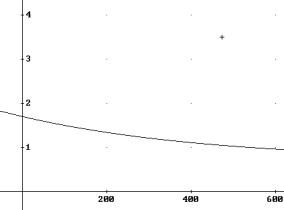
Categorization: KOch/KOde, KUpr/KUsr, JOni/JOtr.

Value of the exercise with symbolic helper: As students are also allowed to use ordinary calculators with exponential function, DERIVE does not bring any additional advantage in the first part. The second part is useless with symbolic computation– we merely press the required key.

Proposed change if symbolic computation is allowed: The same remark as always when solving equations is involved. If procedure for solving is considered to be important, we have to insist on not using Solve and writing all the intermediate steps. If the required height would be 1.6m, the exercisse becomes perhaps more meaningfull. As two last pictures show, the student must explore what is going on, as the height 1.6m is not reached at the end of the jump.

Conclusion

The main benefit of such an analysis is mainly in emphasizing the fact that we must consider what we really want to test with each exercise. For example if we want to test the knowledge of the procedure of solving a linear equation, we must state explicitly that all steps must be clearly written down.

Literature

[Budin, Gaberšček 1999a] Budin J., Gaberšček S., Answers to Conference Issues from Slovenia in Examination and certification system at the end of the upper secondary general education (Electronic conference, May - December 1999) http://www.mss.edus.si/exam/siiss.html

[Budin, Gaberšček 1999b]Budin J., Gaberšček S., Examination and Certification System at the End of Upper Secondary General Education in Slovenia in Examination and certification system at the end of the upper secondary general education (Electronic conference, May - December 1999)

http://www.mss.edus.si/exam/sides.html

[Jones 1995] P. Jones, Graphics calculators in traditional year 12 mathematics testing, in A. Richards (ed.) FLAIR: Proceedings of the 15^th Biennial Conference of the AAMT, 1995, pp. 221-227

[Jones, McCrae 1996] P. Jones, B. McCrae, Assessing the Impact of Graphics Calculators on Mathematics Examinations, Proceedings of the 19th annual conference of the Mathematics Education Research Group of Australasia (MERGA), 1996, Melbourne, Victoria, Australia      http://www.edfac.unimelb.edu.au/DSME/TAME/issues/issue09.pdf

[Kokol 1999] V. Kokol-Voljč, Exam Questions when using CAS for school mathematics teaching, ACDCA 5th Summer Academy, Gösing (Lower Austria), 1999, http://www.acdca.ac.at/kongress/goesing/g_kokol.htm

[Kokol 2000] V. Kokol-Voljč, Examination Questions when using CAS for school mathematics teaching, The International Journal of Computer Algebra in Mathematics Education, Vol 7, No. 1, pp. 63 - 76